Skip to main content

Translate

Statistics Exercise -13.3 (Median)

 Hi Friends and Champs! 

We will discuss about the median for grouped given data in the upcoming exercise. You were already familiar with finding the median for an ungrouped data from the prior class. To determine the median for ungrouped data, follow these steps:

Step-1 Rearrange the given frequency (Data ) in the ascending order.

Step-2  If the total of the given frequency (Data ) is odd then the median is $$\frac {n+1} {2} th\ observation$$ otherwise ( if total is even ) the average of the $$\frac {n} {2} + \left< \frac {n} {2}+1 \right>\ th \ observations$$ Example for the data as given below:   

Observations        Frequency of occurrence

        x1                                      f1

        x2                                      f2

        x3                                      f3

       ---                                      ---

       ---                                      ---

       xn                                       fn

Median for the above ungrouped data when f1,f2,......fn are in ascending order is:

$$\frac {n+1} {2} th\ observation\ if\ n\ is\ odd$$ else the average of $$\frac {n} {2} + \left< \frac {n} {2}+1 \right>\ th \ observations,\ if\ n\ is\ even$$.
Now for the grouped data , this may be difficult to find the median in the usual way , because the median value will be somewhere within the class interval. So to find the median for grouped data , we first find the median class , with the help of c.f. ( cumulative frequency) method. Cumulative meaning is successive addition i.e. we add the successive frequency with the previous one, for more clearance, please check the following table:

Observations        Frequency of occurrence            Cumulative Frequency (c.f.)

        x1                                      f1                                                    f1                                                

        x2                                      f2                                                f1+f2f

        x3                                      f3                                               f1+f2+f3

       ---                                      ---

       ---                                      ---

       xn                                       fn                                            f1+f2+f3+ -----+ fn

__________________________________________________________

Total                                                                 N = f1+f2+f3+ -----+ fn

__________________________________________________________ 

Let N is the total of c.f. then, we use the formula as given above for ungrouped data to find the median class, i.e.

$$The\ median\ class\ is\ "\ whose\ cumulative\ frequency\ is\ greater\ than\ or\ nearby\ to\ \frac {N} {2}"$$

After that, we use the following formula to find the median:

$$Median\ =\ l+\ \frac {\frac {N} {2} - cf} {f} ×\ h$$where l = lower limit of median class,

N = number of observations,
cf = cumulative frequency of class preceding the median class,
f = frequency of median class,
h = class size (assuming all class size is equal).
$$A\ very\ beautiful\ relationship\ among\ all\ three\ central\ tendanacy\ measures\ is$$ $$3\ Median\ =\ Mode\ +\ 2\ Mean$$
Now let's do the next exercise.$$Exercise-13.3$$
1. The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them:
Solution:
$$\because\ cumulative\ frequency\ N=68\ hence\ average\ of\ \frac {N} {2}\ th\ and \frac {N} {2} +1\ th$$ $$i.e.\ average\ of\ 34\ +\ 35\ =\ 69\ is\ \frac {69} {2}=\ 34.5$$ $$which\ near\ by\ class\ is\ 125-145$$ $$hence\ l=\ 125,\ N=68,\ cf\ =\ 22\ (preceding\ c.f.),\ h=20,\ f=20$$ $$\because\ Median\ =\ l+\ \frac {\frac {N} {2} - cf} {f} ×\ h$$ $$\therefore\ Median\ =\ 125+\ \frac {\frac {68} {2} - 22} {20} ×\ 20$$ $$\therefore\ Median\ =\ 137$$ For calculating Mean and Mode use the below formulas as we used in previous exercise:
\[\because \ x̅ =\ a+\ h\frac{Σfiui} {Σfi} \] \[\therefore \ x̅ =\ 135+\ 20\frac{7} {68} \] \[\therefore \ x̅ =\ 135+\ 20×{0.1029} \] \[\therefore \ x̅ =\ 137.058\ Mean\ Value \] Ans
and Mode is: \[\because Mode=l + \frac{f1-f0} {2f1-f0-f2}×h \] \[\therefore Mode=125 + \frac{20-13} {2×20-13-14}×20 \] \[\therefore Mode=135.769\ Mode\ Value \] Ans.
So all the three measures are approximately same.
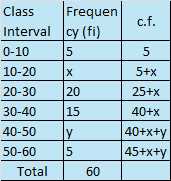
2. If the median of the distribution given below is 28.5, find the values of x and y.
Solution:
Median =28.5 (given)

$$\because Total\ of\ all\ the\ frequencies\ is\ =\ 60$$
$$\therefore 60=45+x+y$$
$$\therefore x+y=15\ --------\ (1)$$
$$\because median\ is\ 28.5\ which\ will\ exist\ in\ class\ 20-30$$
$$\therefore l=20,\ h=10,\ cf=5+x,\ f=20,\ \frac {N} {2} =30$$
$$\because\ Median\ =\ l+\ \frac {\frac {N} {2} - cf} {f} ×\ h$$
$$\therefore\ 28.5=20+\ \frac {30-(5+x)} {20} ×10$$
$$\therefore\ 57=40+\ 30-(5+x)$$
$$\therefore\ x=8\ Ans.$$
$$from\ equation\ (1)\ by\ putting\ value\ of\ x$$
$$y=7\ Ans.$$
3. A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 year.
Solution:
$$\because\ Median\ =\ l+\ \frac {\frac {N} {2} - cf} {f} ×\ h$$
$$\therefore\ Median=35+\ \frac {50-45} {33} ×5$$
$$\therefore\ Median=35+\ 0.757$$
$$\therefore\ Median=35.757\ Age\ Ans.$$
4. The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and the data obtained is represented in the following table :
Find the median length of the leaves. (Hint : The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5 - 126.5, 126.5 - 135.5, . . ., 171.5 - 180.5.)
Solution: We first convert the given data in continuous classes form, because we have the formula for continuous classes, then will find the c.f. class.
$$\because\ Median\ =\ l+\ \frac {\frac {N} {2} - cf} {f} ×\ h$$
$$\therefore\ Median=144.5+\ \frac {20-17} {12} ×9$$
$$\therefore\ Median=144.5+\ 0.25$$
$$\therefore\ Median=144.75\ mm\ Ans.$$
5. The following table gives the distribution of the life time of 400 neon lamps :

Find the median life time of a lamp.
Solution:
$$\because\ Median\ =\ l+\ \frac {\frac {N} {2} - cf} {f} ×\ h$$
$$\therefore\ Median=3000+\ \frac {200-130} {86} ×500$$
$$\therefore\ Median=3000+\ 406.976$$
$$\therefore\ Median=3406.976\ Hours\ Ans.$$
6. 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
Determine the median number of letters in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.
Solution:
$$\because\ Median\ =\ l+\ \frac {\frac {N} {2} - cf} {f} ×\ h$$
$$\therefore\ Median=7+\ \frac {50-36} {40} ×3$$
$$\therefore\ Median=7+\ 1.05$$
$$\therefore\ Median=8.05\ \ Ans.$$
7. The distribution below gives the weights of 30 students of a class. Find the median weight of the students.
Solution:
$$\because\ Median\ =\ l+\ \frac {\frac {N} {2} - cf} {f} ×\ h$$
$$\therefore\ Median=55+\ \frac {15-13} {6} ×5$$
$$\therefore\ Median=55+\ 1.67$$
$$\therefore\ Median=56.67\ kg\ Ans.$$

I hope all the questions are properly readable and understandable, in case of some confusion, kindly let me know in comment section 🙏🙏🙏







Labels:

Comments

Post a Comment

Popular posts from this blog

Statistics Exercise -13.1

Hi Friends and Champs! In the next exercise, we will talk about the mean or average for given data. You already learn about the mean for the ungrouped data in the previous class: Example for the data as given below:    Observations           Frequency of occurrence           x 1                                                   f 1           x 2                                                  f 2           x 3                                       ...
Post a Comment
Read more

Pair of Linear Equation in two variables Exercise - 3.3 Elimination Method

Hi Friends and Champs! In the next exercise, we will solve the questions by the elimination method.                                                                 EXERCISE 3.3.  1. Solve the following pair of linear equations by the elimination method and the substitution method :         (i) x + y = 5 and 2x – 3y = 4                          (iii) 3x – 5y – 4 = 0 and 9x = 2y + 7         (ii) 3x + 4y = 10 and 2x – 2y = 2                  (iv) x/y +  2y/3 = -1 and x - y/3 = 3 Solution:  (i)  x + y = 5 --------------- (1)        2x – 3y = 4  -------------(2) Multiply ...
3 comments
Read more

Arithmetic Progressions Exercise 5.3

 Hi Friends and Champs! Before proceeding to the next exercise, we need to understand the following: The general form of an AP is : a, a+d, a+2d, a+3d, ..................................,a+(n-1)d Let S is the sum of first n term of the above given AP then, S n  = a + (a+d) + [ a + 2d ] + [ a+ 3d ] + ---------------------+ [ a+(n-2)d]+ [ a+ (n-1)d] ----------(1) let reverse the order of eq(1), we have, S n = [ a+(n-1)d ] + [ a + (n-2)d ] + -----------------------------+ (a+2d) + (a+d) + a -----------------(2) Adding eq (1) and (2), we have 2 S n  = [ 2a+(n-1)d ] + [ 2a+(n-1)d ]+ [ 2a+(n-1)d ]+ [ 2a+(n-1)d ]+ [ 2a+(n-1)d ]+++++  n times => 2 S n  = n[ 2a+(n-1)d ] =>  S n  = n/2[ 2a+(n-1)d ] the sum of first n terms of an AP As we already know , that if " l " is the last term of an AP of n terms then l = a + (n-1)d So  S n  = n/2[2a + (n-1)d] =>  S n  = n/2[ a+ {a +(n-1)d}] =>   S n  = n/2[a + l ]     ...
Post a Comment
Read more

Quadratic Equation Exercise 4.2

Hi Friends and Champs! Before to begin next exercise, we need to understand some basic points, for solving the problems easily. As you know the general equation for quadratic equation is: ax 2 +bx+c=0, a ≠ 0 To factorize  Step -1:  Multiply coefficient of  x 2   with constant term i.e. multiply "a" and "c". Step-2:  Factorize middle term or coefficient of x, such that the multiplication should be equal to the result obtained from multiplication of "a" and "c" and addition or subtraction should be equal to the middle term coefficient "b".  Ex:    x 2 +5x+6=0  Step -1:  Multiply coefficient of x 2   with constant term i.e. multiply "a" and "c",                 i.e. 1 x 6 =6 Step -2:  3 + 2 =5 (middle term coefficient)               3 x 2 = 6 (multiplication of "a" and "c")          ...
Post a Comment
Read more

NCERT Class 10 Math Quadratic Equation Exercise 4.3

 Hi Friends and Champs! Before We start next exercise, need to give some attention on below considerations: As you know the general equation of a quadratic equation is:             ax 2  + bx + c = 0 , a ≠ 0 solve this equation to find the roots or Zeroes for "x" . In above result roots or ZEROES of the general equation ax 2  + bx + c = 0 , a ≠ 0 depend on the value of  (b 2 - 4ac) called  Discriminant  . Now we have 3 cases in this scenario. Ist Case :      When discriminant ( b 2 - 4ac ) > 0 , Roots will be real and distinct. 2nd Case :    When discriminant ( b 2 - 4ac ) = 0, Roots will be identical and real. 3rd Case :     When discriminant ( b 2 - 4ac ) < 0 , Roots will be imaginary and distinct. Exercise: 4.3 1. Find the nature of the roots of the following quadratic equations....
Post a Comment
Read more

Introduction to Trigonometry Ex- 8.1

 Hi Friends and Champs Before we proceed to the next exercise let's understand some basic facts about trigonometry.  Trigonometry is the combination of three Greek words " tri", "gon"  and  " metron"  . " tri"  mean three " gon"  means sides and " metron"  mean measure. So, trigonometry means to study the relationship between sides and angles of a triangle.    Trigonometry Ratios:   Let  Δ ABC is a right angle triangle , right angle at B, then: Sin A = BC / CA           i.e. Side opposite to angle A / Hypotenuse Cos A = AB / CA             i.e. Side adjacent to angle A / Hypotenuse Tan A = BC / AB             i.e. Side opposite to angle A / Side adjacent to angle A  Cosec A = CA / BC      i.e Hypotenuse /. Side opposite to angle A Sec A = CA / AB          i.e. Hypotenuse / ...
Post a Comment
Read more

Learn Excel V-Lookup in Easy Way

Let We have three tables  names:  Table - 1 ( our Main Database Table ) and  Table - 2 Where we have only Name of customer and require Mob No  Table -3 Where we have customer name and require customer City.  VlookUP Function is: VLOOKUP(lookup_value , table_array, col_index_num ,[range_lookup])  lookup_value Attribute : what you want to search.   table_array attribute       : where vlookup funtion will search , Fix data range from database   col_index_num attribute : which column data result you require from selected data range .   range_lookup   attribute    : Either you require exact match for your lookup_value or partial match.                                                                     ...
Post a Comment
Read more

Real Numbers Exercise 1.1

 Hi Friends and Champs, Before coming to the exercise 1.1, we need to understand some points, which you have already read in class IX. Prime Number: Those numbers which could be divide by "1" and itself. i.e. there are only two multiple of the number, example 2,3,5,7...... etc. 2 is the smallest prime number we have. "1" is not a prime number, because for a prime number there should be exactly two multiples of the number, but "1" have only one multiple which is itself. Prime factors: Prime factors are the product of prime numbers for a given number. ex 2x2x3x5 are the prime factors for the number 60.   Exercise 1.1 Q-1 Express each number as a product of its prime factors: (i) 140        (ii) 156    (ii) 3825    (iv)  5005     (v) 7429 Note: Prime numbers are those numbers, which could be divide by 1 and by itself. Note: Do not try to skip the steps in prime factorization, start from the lowest prime number. Solution:...
Post a Comment
Read more

Surface Areas and Volumes Exercise - 12.2

Hi Friends and Champs!  In this chapter, we will learn to find the resulting volumes by joining or scooping of different shape bodies in the same way as in previous exercise. Let's start.  Exercise 12.2 1.A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.  Solution: radius of both cone and hemisphere r = 1 cm height of the cone h = r = 1 cm Volume "v" of the solid = volume of the hemisphere + volume of the cone v = 2/3  πr ³ + 1/3  πr ² h =2/3  π1 ³ +   1/3  π1 ² ×1 = 2/3  π +  1/3  π = π cm ³ Ans. 2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contai...
Post a Comment
Read more

Statistics Exercise -13.2

Hi Friends and Champs! We will talk about the mode of some supplied grouped data today. Remember that you have already learnt the mode for ungrouped data from the last class. As you are previously aware, the mode for ungrouped data is the frequency that is repeated more frequently. As an illustration: Example - Run score by a batsman in 8 matches are 50,98,99,98,76,75,99,98.Find the mode ? Solution : 98 runs repeated 3 times , Hence mode is 98. It is evident from the example above that figure 98 is the mode because it is repeated three times.Thus, it is easy to find the mode for ungrouped data. However, it is a little more complicated with aggregated data. For ungrouped data, we select the class with the highest frequency and use the formula below to determine the mode. \[Mode=l + \frac{f1-f0} {2f1-f0-f2}×h \] where l = lower limit of the modal class, h = size of the class interval (assuming all class sizes to be equal), f1 = frequency of the modal class, f0 = frequency of t...
Post a Comment
Read more